Bei der Wechselstromlehre geht es in erster Linie um die Netzwerkanalyse bei Vorhandensein von Wechselspannungquellen und/oder Wechselstromquellen. Im Gegensatz zur Berechnung von Netzwerken unter Gleichspannung, werden durch Induktivitäten und Kapazitäten unter Wechselspannung elektromagnetische Felder auf und wieder abgebaut. Die dafür benötigte Leistung ist verlustlos und wird darum auch Blindleistung genannt.
In der Wechselstromtechnik werden die unbekannten elektrischen Größen (Teilströme, Teilspannungen) in der Regel im sogenannten komplexen Bildbereich berechnet. Dies ist effizienter als die Berechnung im Zeitbereich, da dort Differentialgleichungen gelöst werden müssten. Voraussetzung zur Transformation der Größen in den komplexen Bildbereich ist, dass es sich um sinusförmige Größen handelt.
In Abb. 1 ist ein einfaches Netzwerk dargestellt, dass von einer Wechselspannungsquelle versorgt wird. Auf der linken Seite wird einmal diese Spannung im Zeitbereich beschrieben und einmal im Bildbereich. Letztendlich wird in der komplexen Wechselstromtechnik mit dem komplexen Effektivwert gerechnet.
Die komplexe Sinusspannung kann in einem Zeigerdiagramm im komplexen Koordinatensystem dargestellt werden (siehe Abb. 1 oben mittig). Dieser Zeiger dreht sich mit der Zeit. Projiziert man die Spitze des Zeigers auf die Zeitachse, so ergibt sich wieder die Sinusspannung im Zeitbereich (siehe Abb. 1 oben rechts). Der komplexe Effektivwert dreht sich nicht, er liegt mit dem Übertragungswinkel im komplexen Koordinatensystem, in diesem Beispiel ist der Übertragungswinkel der Spannung 0°. Der komplexe Effektivwert des Stroms hat einen Winkel <0°, dieser „eilt“ der Spannung nach.
Abb. 1 zeigt rechts unten die Berechnung des Netzwerks, die Berechnung im Zeitbereich wird nur angedeutet. Es ist aber zu erkennen, dass die Berechnung im Bildbereich weitaus einfacher erscheint. Hat man die Größen im komplexen Bildbereich berechnet können diese wieder in den Zeitbereich übertragen werden. Für die Rücktransformation in den Zeitbereich kann einfach der Imaginärteil der berechneten komplexen Größe in Polarform genommen werden vice versa zu dem ersten Schritt der Transformation von Zeit- in den Bildbereich wie in Abb.1 dargestellt.
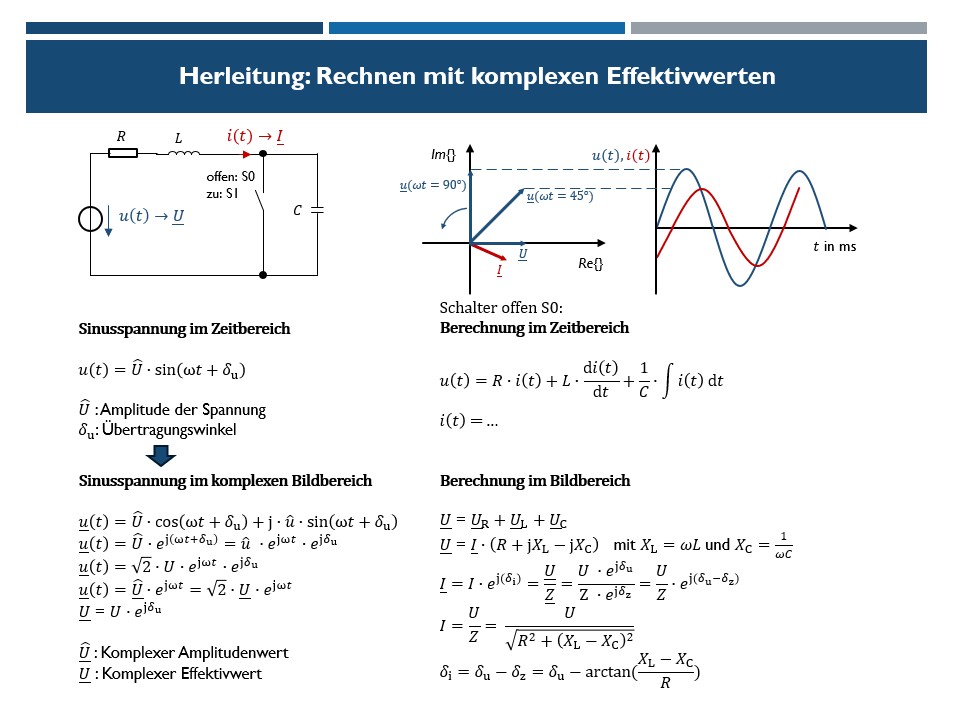
Abb. 1: Herleitung zum Rechnen mit komplexen Effektivwerten